Particle Filters
Master the go-to method for AMR localization. Particle Filters use Monte Carlo tricks to nail position estimates in messy, changing spaces where sensors and odometry falter.

Core Concepts
The Particle
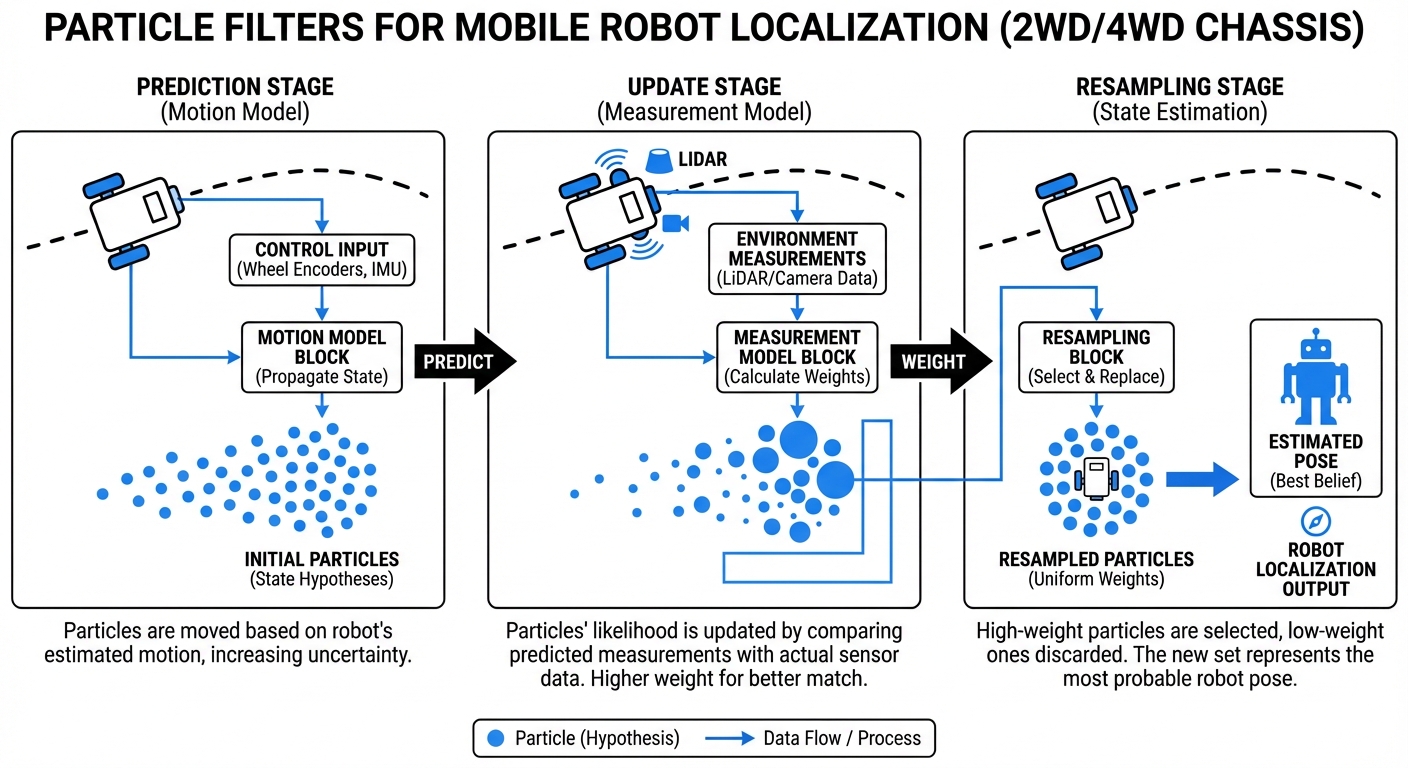
Each particle is a guess at the robot's state (x, y, θ). More particles in a spot mean higher odds that's where it is.
Motion Model
As the robot rolls, particles shift with odometry, plus some noise for wheel slip and drift.
Sensor Model
Sensors like LiDAR or cameras scan, and particles get weights—ones matching the map score higher.
Resampling
Survival of the fittest: Ditch low-weight particles, clone the winners to zero in on probable spots.
Convergence
Eventually, particles bunch up right at the true position, delivering spot-on localization even from fuzzy starts.
Global Localization
Unlike Kalman filters, particle filters nail the "Kidnapped Robot" problem—they can re-localize your AGV even if someone picks it up and hauls it somewhere new.
How It Works: MCL
Monte Carlo Localization (MCL) leans on the law of large numbers. Forget chasing a single "best guess" spot; your AGV juggles a whole cloud of probabilities.
1. Prediction:
2. Correction: would
3. Resampling:
Real-World Applications
Warehouse Logistics
In those mirror-image warehouse aisles where pillars all blend together, particle filters keep multiple location guesses alive until a standout landmark—like a charging station or quirky wall—clears things up.
Hospital Delivery Robots
Hospitals mean endless hallways and constant foot traffic. Particle filters shrug off moving people blocking the view, keeping the robot locked on its spot in the facility map.
Manufacturing Floors
When pallets and machines shuffle around a lot, the probabilistic smarts of particle filters stop the robot from freaking out over small map mismatches and getting 'lost.'
Last-Mile Delivery
Outdoor sidewalk robots? Particle filters blend GPS, odometry, and camera feeds to stay spot-on, even when GPS flakes out in city canyons.
Frequently Asked Questions
What sets a Kalman Filter apart from a Particle Filter?
Kalman Filters (like EKF/UKF) assume a linear world with nice Gaussian errors (that bell curve vibe). Particle Filters go non-parametric, handling any wild distribution—perfect for 'multi-modal' scenarios where the robot could be in two spots at once.
Why are Particle Filters considered computationally expensive?
It scales right with particle count. Running thousands (say, 2,000 to 5,000) through simulation, scoring, and resampling every sensor ping? That's way hungrier on CPU than Kalman Filter's quick matrix crunching.
What is the "Kidnapped Robot Problem"?
This is when someone grabs the robot, moves it blind, and drops it elsewhere. A tuned particle filter bounces back by scattering random particles map-wide, letting sensors zero in on the real spot.
How many particles should I use for my AGV?
Depends on your space and hardware. Tiny room? 500-1,000 particles do the trick. Massive warehouse (10,000+ sq ft)? Crank it to 5,000+. AMCL smartly tweaks the count based on how confident it feels.
Does a Particle Filter require a static map?
Usually, yeah. Classic MCL pits sensor reads against a fixed occupancy grid. Smarter versions filter out movers (like folks) before scoring, tackling semi-dynamic spots.
What represents a "Particle" in code?
A particle's basically a lightweight struct: X (float), Y (float), theta/heading (float), and weight (float). The filter wrangles an array of 'em.
What is "Particle Depletion"?
Depletion hits when resampling wipes out particles near the truth—maybe from overly harsh sensor models or too few particles total. Robot goes 'delocalized' and needs a reset to recover.
Can Particle Filters work with Cameras instead of LiDAR?
Totally. LiDAR does geometry matches, but visual versions pit camera pics against image maps or landmarks. Core math's identical; just swap the weighting (sensor update) step.
How do we handle initialization?
Yep. User kicks it off with a guess (like 'at the charger'). Particles spawn in a Gaussian blob around there. No clue? Spread 'em evenly map-wide for global localization.
Is AMCL the same as a Particle Filter?
You bet. AMCL (Adaptive Monte Carlo Localization) rules ROS. 'Adaptive' means it ramps particles up or down based on how well sensors match.