Kalman Filters
The ultimate algorithm for sensor fusion and state estimation in mobile robotics. Conquer uncertainty with razor-sharp math, so your AGVs glide smoothly and spot-on through chaotic spaces.

Core Concepts
State Estimation
Figuring out a system’s hidden secrets—like a robot’s true position and speed—that sensors can’t measure perfectly on their own.
Sensor Fusion
Merging data from different sources (wheel encoders, IMU, LiDAR) for a result way sharper than any solo sensor.
Gaussian Noise
Real sensors are messy and noisy. Kalman filters model that noise as a Gaussian bell curve, letting math wipe out the random junk.
Prediction Step
It taps a physics model to predict where the robot *ought* to be next, using its last known state and inputs like motor commands.
Correction Step
It grabs fresh sensor readings, pits them against the prediction, and tweaks the estimate based on the sensor’s reliability.
Covariance Matrix
A math snapshot of uncertainty—tracking the robot’s confidence in x, y, and theta, tightening up as solid data rolls in.
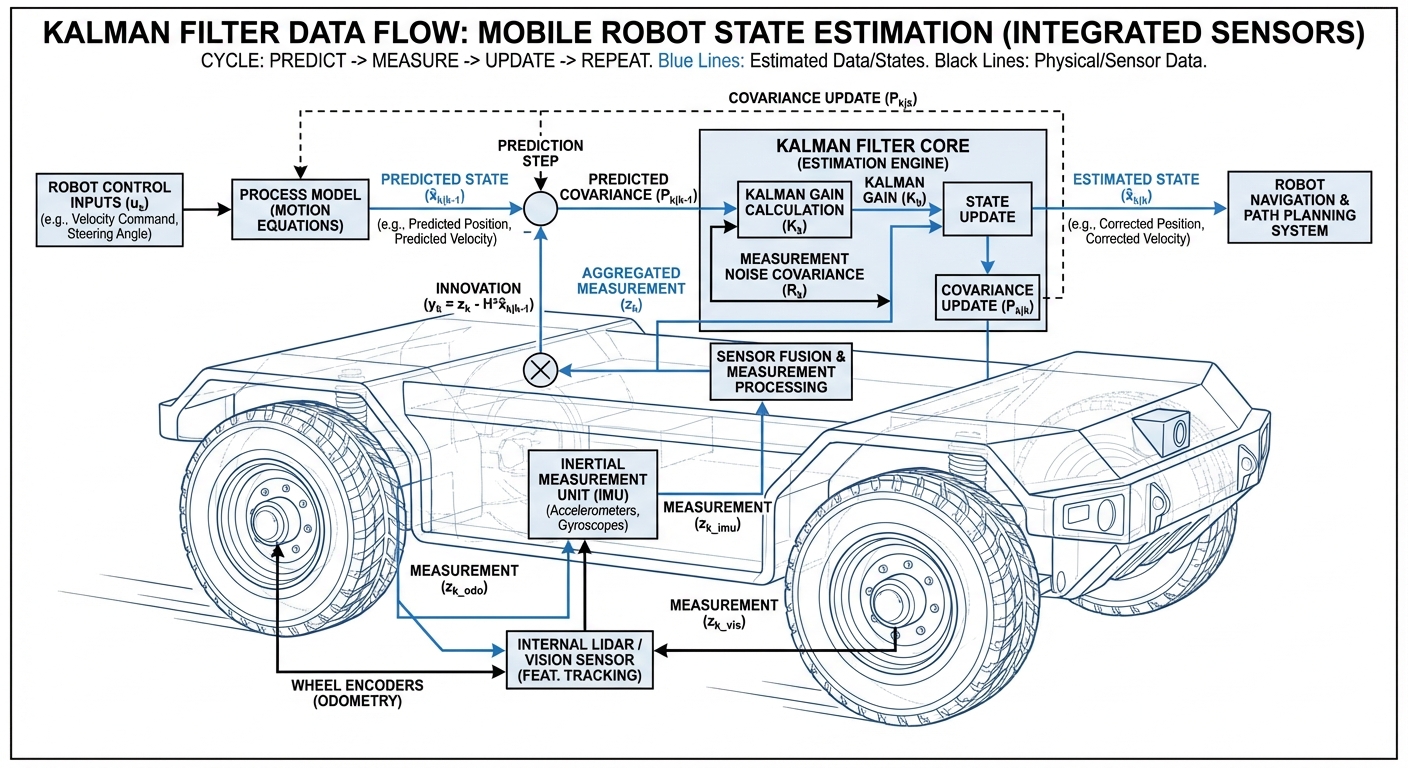
How It Works: The Loop
The Kalman Filter’s magic is its endless predict-update loop, firing hundreds of times a second in robotics. First, the robot its spot from wheel odometry (dead reckoning). Wheels slip, though, so errors pile up.
Next, it with absolute sensors like LiDAR or GPS—accurate but noisy, no drift.
The filter blends them via the Kalman Gain: trust sensors more if they’re solid, lean on prediction if they’re iffy. Boom—silky, dead-accurate path.
Real-World Applications
Warehouse Logistics
AMRs fuse wheel encoders and downward cameras with Kalman Filters to fight drift on slick floors, nailing docking at conveyors.
Outdoor Navigation
Yard tractors and delivery bots tame jumpy GPS near skyscrapers using Extended Kalman Filters (EKF) blended with IMU accel data.
Drone Stabilization
Drones live on Kalman Filters for orientation, fusing quick-drifting gyros with noisy-but-steady accelerometers for steady hovers.
Collaborative Safety
In busy environments with people around, robots track moving obstacles like walking humans. Kalman Filters predict where that person is headed next, letting the robot plan a smooth avoidance path ahead of time.
Frequently Asked Questions
What's the difference between a Kalman Filter and an Extended Kalman Filter (EKF)?
A regular Kalman Filter assumes everything's linear—like straight lines. But robots curve around and use trig-based sensors. The Extended Kalman Filter (EKF) fixes that with Jacobian matrices to locally linearize those non-linear parts, making it the industry standard for most mobile robot navigation.
Why not just use GPS or LiDAR directly, skipping the filter?
Sensors aren't perfect. GPS updates slowly (1-10Hz) and can jump meters in an instant. LiDAR gets tricked by glass or mirrors. A Kalman Filter bridges slow updates with faster ones (like IMUs) and statistically ignores outliers, stopping the robot from jerking around wildly.
How computationally expensive is a Kalman Filter?
It's incredibly efficient. Unlike Particle Filters (MCL) that juggle thousands of possible robot poses at once, a Kalman Filter just tracks one pose and its uncertainty. Perfect for embedded microcontrollers and real-time AGV ops.
What happens if a sensor fails completely?
Kalman Filters handle sensor dropouts like champs. If a correction source (say, a camera) fails, it falls back on predictions (dead reckoning). Uncertainty grows over time, but the robot keeps moving instead of halting right away.
What are those Q and R matrices you see in the docs?
They're the filter's tuning knobs. Q covers process noise—like how much the robot slips or wobbles. R is measurement noise—sensor inaccuracies. Nail these, and you tell the filter which data to trust more.
Can a Kalman Filter solve the "Kidnapped Robot" problem?
Generally, no. Kalman Filters are local optimizers—they shine at tracking if you start with a good position. Get kidnapped (picked up and moved)? It'll diverge fast. For global localization, Particle Filters (MCL) step in to reset.
How does it handle IMU drift?
IMUs measure acceleration, but double-integrating to position causes huge drift fast. Kalman Filters use IMUs for high-frequency, short-term updates and tame the drift with slower, absolute fixes from odometry or LiDAR for the long term.
Is it used for SLAM (Simultaneous Localization and Mapping)?
Yes, especially in EKF-SLAM. The state vector covers not just robot position, but landmark coordinates too. As it moves, the filter updates both position and map together.
Does it work with non-Gaussian noise?
Standard Kalman Filters expect Gaussian (bell curve) noise. Multi-modal noise—like a sensor that sometimes totally lies—trips them up. That's when Unscented Kalman Filters (UKF) or Particle Filters work better.
How do I implement this in ROS 2?
The go-to package is `robot_localization`. It delivers a solid EKF out of the box. Configure via YAML: pick sensors (Odom, IMU, GPS) to fuse and set covariance thresholds.