Jacobian Matrix
The math link turning wheel speeds into exact robot motion. Crucial for buttery path planning and kinematic control in cutting-edge AGV fleets.

Core Concepts
Velocity Mapping
Instantly connects joint space (wheel spins) to Cartesian space (chassis speed/rotation).
The Inverse Jacobian
Key for control loops. Invert to J^{-1} and solve for motor speeds to nail any desired trajectory.
Singularity Analysis
Flags robot poses losing a degree of freedom. In mobile manipulators, skip these to avoid control blackouts.
Static Force Transmission
Jacobian transpose uses virtual work to convert chassis forces back to wheel torques.
Non-Holonomic Constraints
For diff-drive AGVs, it embeds no-sideslip constraints, pruning the null space to what's doable.
Mecanum Drive Matrix
In omnidirectional robots, the Jacobian has full rank, letting them translate in X and Y while rotating around theta all at the same time.
How It Works
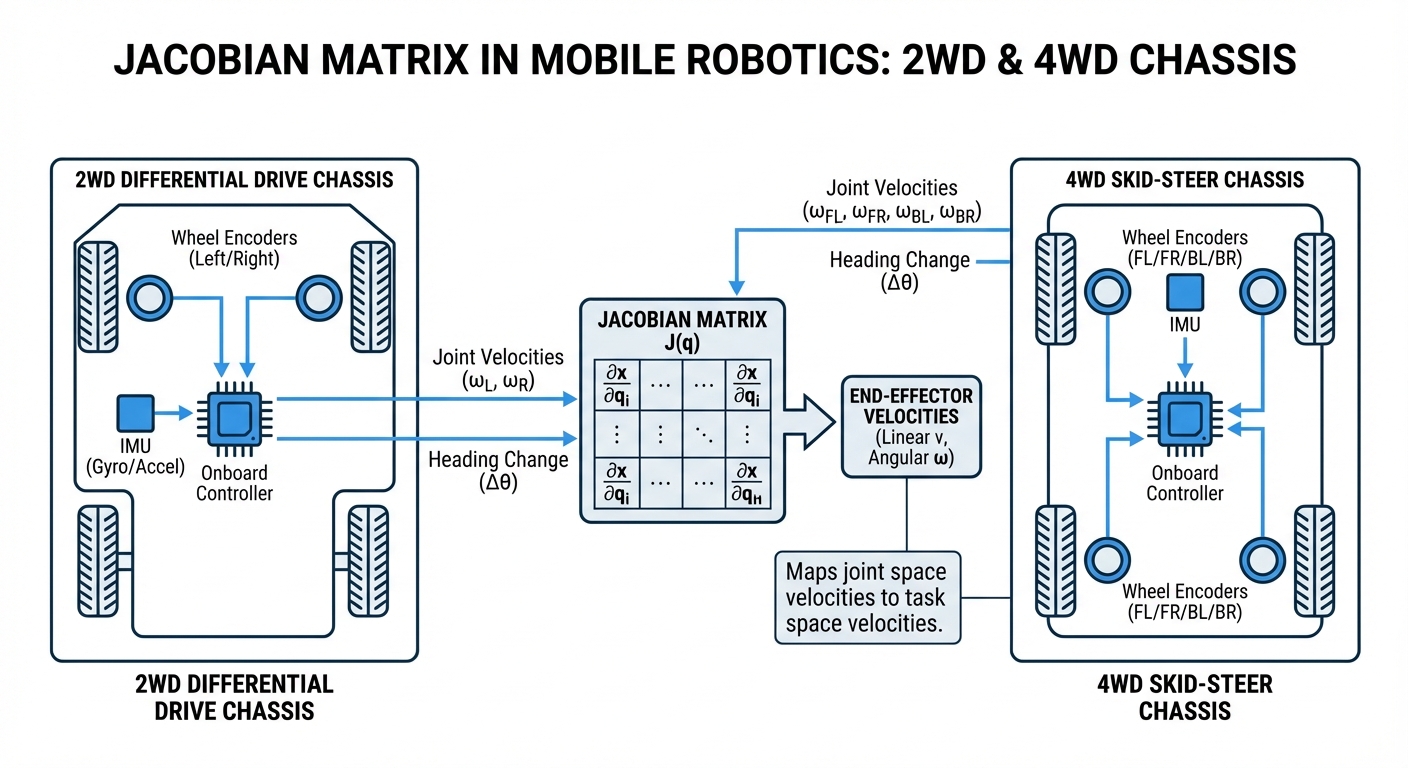
The Jacobian matrix ($J$) is basically a linear transformation that connects wheel speeds to the robot's motion. For a differential drive AGV, it links the left and right wheel angular velocities ($\dot{\phi}_L, \dot{\phi}_R$) to the linear velocity ($v$) and angular velocity ($\omega$) right at the robot's center.
Mathematically, it's $\dot{x} = J \cdot \dot{q}$. Here, $\dot{x}$ is the task space vector—how fast the robot's zipping around in the real world—and $\dot{q}$ is the configuration space vector, or how quickly the wheels are spinning.
By crunching this equation nonstop in real-time control loops (usually 50Hz to 1000Hz), the robot's controller keeps the wheels locked onto the navigation software's planned path, handling geometry and kinematic limits along the way.
Real-World Applications
Precision Docking
AGVs need sub-millimeter precision to dock perfectly with conveyors or charging stations. The Jacobian makes those tiny wheel speed tweaks possible for spot-on chassis alignment with external markers.
Mobile Manipulation
Robots with arms on mobile bases use a "Whole Body Jacobian" to tie the base motion to the arm's, so the arm can snag objects even while the base is still cruising.
Omnidirectional Navigation
Warehouse robots with Mecanum wheels rock a 3x4 Jacobian matrix (for four wheels). It unlocks slick moves like sideways strafing into tight aisles without twisting the chassis.
Dynamic Obstacle Avoidance
When someone steps in front of an AGV, the local planner spits out a fresh velocity vector. The Inverse Jacobian snaps it into motor commands for a buttery-smooth swerve.
Frequently Asked Questions
What is the Jacobian Matrix in simple terms?
Picture it as a sensitivity map or a "gear ratio" for fancy multi-axis moves—it spells out exactly how much the robot shifts if you nudge one wheel just a smidge.
Why do I need the Inverse Jacobian?
The regular Jacobian figures robot speed from wheel speed. But control software flips it: you pick your goal motion (task space), and the Inverse Jacobian crunches the wheel speeds to make it happen.
What happens if the Jacobian Matrix is not square?
When the matrix isn't square (say, a redundant robot with extra motors beyond degrees of freedom), no simple inverse works. That's where the Moore-Penrose Pseudoinverse ($J^+$) shines, nabbing the optimal solution that cuts energy or extra motion.
How does wheel slippage affect the Jacobian calculations?
The basic Jacobian assumes flawless traction and rigid mechanics. Real-world AGVs? They slip. Pro controllers deploy Kalman Filters to gauge slip and tweak the Jacobian live, or fuse IMU data to fix position estimates.
What is a singularity in the context of mobile robots?
Standard differential drive robots rarely hit singularities. But steerable-wheel setups (like swerve drives) do when wheels align in a way that blocks instant motion in one direction—you've got to reconfigure the angles first.
Does the Jacobian change as the robot moves?
For fixed-wheel AGVs, the Jacobian often stays constant in the robot's local frame. In the global world frame, though, it hinges on the current heading ($\theta$), so you recalculate it every timestep.
What is the difference between Forward Kinematics and the Jacobian?
Forward Kinematics goes position to position (like wheel angles to robot X,Y spot). The Jacobian handles to (wheel RPM to robot speed). It's really just the derivative of those Forward Kinematics equations.
How computationally expensive is calculating the Jacobian?
For mobile bases, it's super lightweight computationally—small matrices (usually 3x2 or 3x4). It flies on low-power microcontrollers (like STM32) at high rates (>1kHz) with zero drama.
Can I use the Jacobian for torque control?
Yes. Via the principle of virtual work, the Jacobian's transpose ($J^T$) connects forces on the end-effector (or chassis) to torques at the joints (wheels). It's essential for impedance control or compliance.
How does a Differential Drive Jacobian differ from a Mecanum Jacobian?
A Differential Drive Jacobian has a "null space" for side-to-side movement—the math proves $v_y$ is impossible. A Mecanum one is fully loaded, revealing how wheel combos drive $v_x$, $v_y$, and $\omega$ all together.
What role does the Jacobian play in odometry?
Odometry taps the Forward Jacobian. Grab wheel velocities ($\dot{q}$) from encoders, multiply by $J$ for robot velocity estimate, then integrate over time to track position on the map.
How do I troubleshoot Jacobian errors in my code?
Dead giveaways: the robot spins in place on a straight command or backs up unexpectedly. Scrutinize those matrix row signs (+/-)—they depend on motor mounting and positive rotation definitions.