Inverse Kinematics
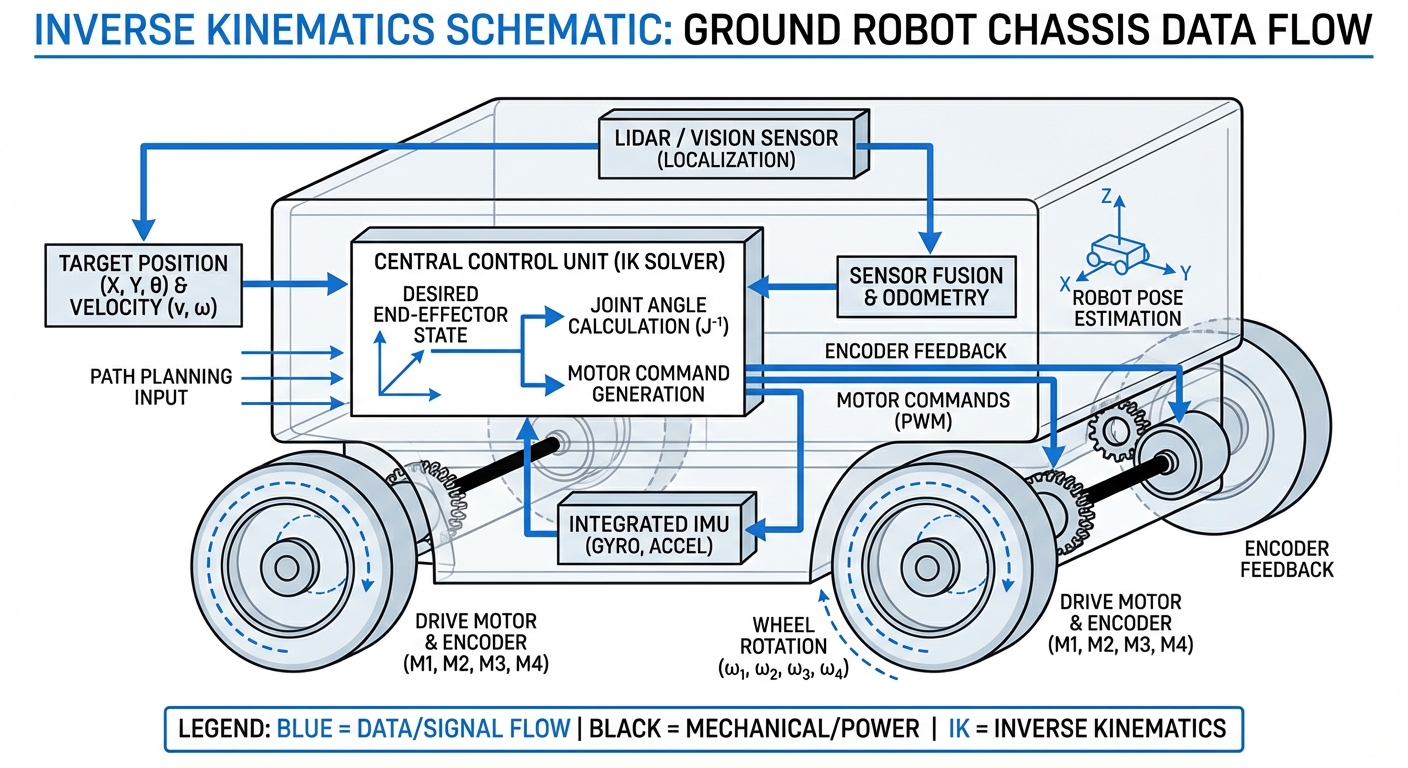
Inverse Kinematics (IK) is the math wizard bridging a robot's dream path to its real-world motors. It converts high-level 'go here' commands into spot-on wheel speeds, letting AGVs tackle tricky spaces with sub-millimeter precision.

Core Concepts
Task Space
That's the target spot in x, y coordinates plus orientation (theta). IK kicks off here, figuring the exact move needed against the global map.
Configuration Space
The lineup of joint or wheel settings. On a mobile robot, it's the precise speeds for each motor to nail the job.
The Jacobian Matrix
A matrix of partial derivatives linking joint speeds to end-effector motion. It's the computational powerhouse for real-time IK in navigation.
Holonomic Constraints
This decides if your robot can scoot any direction (like with omni-wheels) or handles like a car (differential drive). The IK math shifts big-time based on these limits.
Closed-Loop Control
IK sets the goal speeds. Then PID controllers watch encoders and IMUs to make sure the wheels actually hit those marks.
Singularities
Tricky math spots where the robot loses a freedom degree. Smart IK solvers spot these ahead to dodge wild moves or total freezes.
How It Works: The Calculation
Picture your fleet software barking: 'Head north at 1.0 m/s, spin 45 degrees.' The AGV's brain can't just relay that straight to the motors.
Enter the Inverse Kinematics algo. It crunches the robot's layout—like wheelbase and track width—to spit out exact RPMs for left versus right wheels.
On a basic differential drive, turning right means left wheel spins faster than right. Mecanum wheels? Way more intricate vector sums for sideways slides without spinning.
This math runs hundreds of times a second, tweaking for tiny path fixes to keep the robot glued to its digital line.
Real-World Applications
Precision Warehouse Docking
AGVs lean on inverse kinematics for pinpoint dockings—like matching charging ports or belts with millimeter accuracy. IK nails those final angle tweaks for a flawless connect.
Dynamic Obstacle Avoidance
In hectic factories, routes shift on a dime. IK instantly turns fresh nav plans into motor moves, letting bots glide around people or forklifts smoothly.
Medical & Hospital Transport
Hauling delicate bio-samples? No jerky rides. Fancy IK smooths accel ramps so liquids stay calm through sharp turns.
Omnidirectional Assembly
Heavy manufacturing with mecanum wheels? IK crunches the vector wizardry for side-shuffles or pivots, perfect for assembling big parts in snug spots.
Frequently Asked Questions
What is the difference between Forward and Inverse Kinematics?
Forward kinematics figures position from wheel spins (odometry). Inverse kinematics flips it: desired spot or speed becomes the wheel moves to make it real.
Why is Inverse Kinematics difficult for non-holonomic robots?
Non-holonomic bots (cars or diff-drive AGVs) can't sidestep instantly. IK solvers weave in constraints, often curving paths (Bezier or Dubins) to hit side targets.
How does wheel slippage affect Inverse Kinematics calculations?
IK assumes grip like glue, but slips happen. When wheels skid, commands miss the mark. Tough setups loop in IMU or LiDAR (SLAM) feedback to fix the gap between plan and reality.
What is the computational load of IK on an embedded MCU?
For mobile bases, it's lightweight—runs smooth on basics like STM32 or ESP32. But slap a 6-axis arm on an AGV? Those iterative solvers (Newton-Raphson style) hog CPU and need beefy industrial PCs.
How does a mecanum wheel AGV differ in IK mathematics?
Mecanum bots rock three freedoms (x, y, rotation) versus diff-drive's two. Their IK matrix is 4x3, blending wheel forces so you strafe sans spin.
Does changing wheel diameter require re-coding the IK?
Yes, absolutely. Wheel radius is core to velocity ($v = \omega \times r$). Worn treads or swaps? Update params, or you'll always undershoot or overshoot.
What happens at a singularity point?
A singularity is when the Jacobian matrix flops rank—no unique solution (or infinite ones), like a stretched arm. Rare on mobile bases, but steering setups can lock up if wheels sync wrong.
Can IK handle uneven terrain?
Standard planar IK expects flat ground. Bumpy terrain shifts wheel contact, messing calcs. Pro AGVs swap in 3D models and suspension sensors to tweak for hills and dips on the fly.
Is ROS (Robot Operating System) required for IK?
No, IK is straight math—code it in C++, Python, or PLC. ROS speeds things with Navigation Stack libraries that hide the hairy bits for quicker builds.
How does "Ackermann Steering" IK differ from Differential Drive?
Ackermann steering (car-style) links front wheel angles to rear speed, capping tight turns. Diff-drive spins in place ($r=0$), easing math for super-snug spots.
What role do encoders play in IK?
Encoders check IK's work. It demands speeds, drivers push for them, encoders report reality. PID shrinks the gap between setpoint and feedback.
How accurate is IK for long-distance navigation?
IK solo drifts over long hauls from tiny errors piling up. It's for local control; global fixes like LiDAR or QR codes refresh position to feed the IK loop.