A* Path Planning
The champ of pathfinding algorithms. A* blends speed and smarts to steer AGVs through mazes, nailing shortest paths while dodging obstacles on the fly.

Core Concepts
Grid Representation
The world gets sliced into a grid of nodes—open spaces or walls—setting up the search playground.
Heuristic Function (h)
The 'smart' bit: it guesses distance from current spot to goal, zeroing in on winners instead of blind BFS like Dijkstra.
Cost Calculation (f = g + h)
Total cost (f) = path so far (g) + goal estimate (h). Guarantees the optimal route.
Obstacle Inflation
To dodge bumps, 'inflate' obstacles by robot radius in the map. Creates safe clearance for the whole AGV body.
Optimality & Completeness
A* is proven: if a path exists, it'll find it (complete), and it'll be the shortest (optimal) with a solid heuristic.
Open & Closed Sets
The algorithm juggles two key lists: the 'Open Set' for nodes waiting to be checked, and the 'Closed Set' for ones we've already evaluated. This keeps things from looping forever or wasting time on repeats.
How It Works
A* explores the space like a wave, but it's cleverly biased toward the goal. It kicks off at the starting node and checks out the neighboring cells.
For each neighbor, it crunches the movement cost so far (G) plus a smart guess at the distance left (H). Then it picks the one with the lowest total cost (F) to tackle next. It keeps this up until it reaches the goal.
The magic for AGVs? It all happens in milliseconds. Once it hits the goal, it traces back through 'parent' pointers to piece together the exact path of coordinates for the robot to follow.
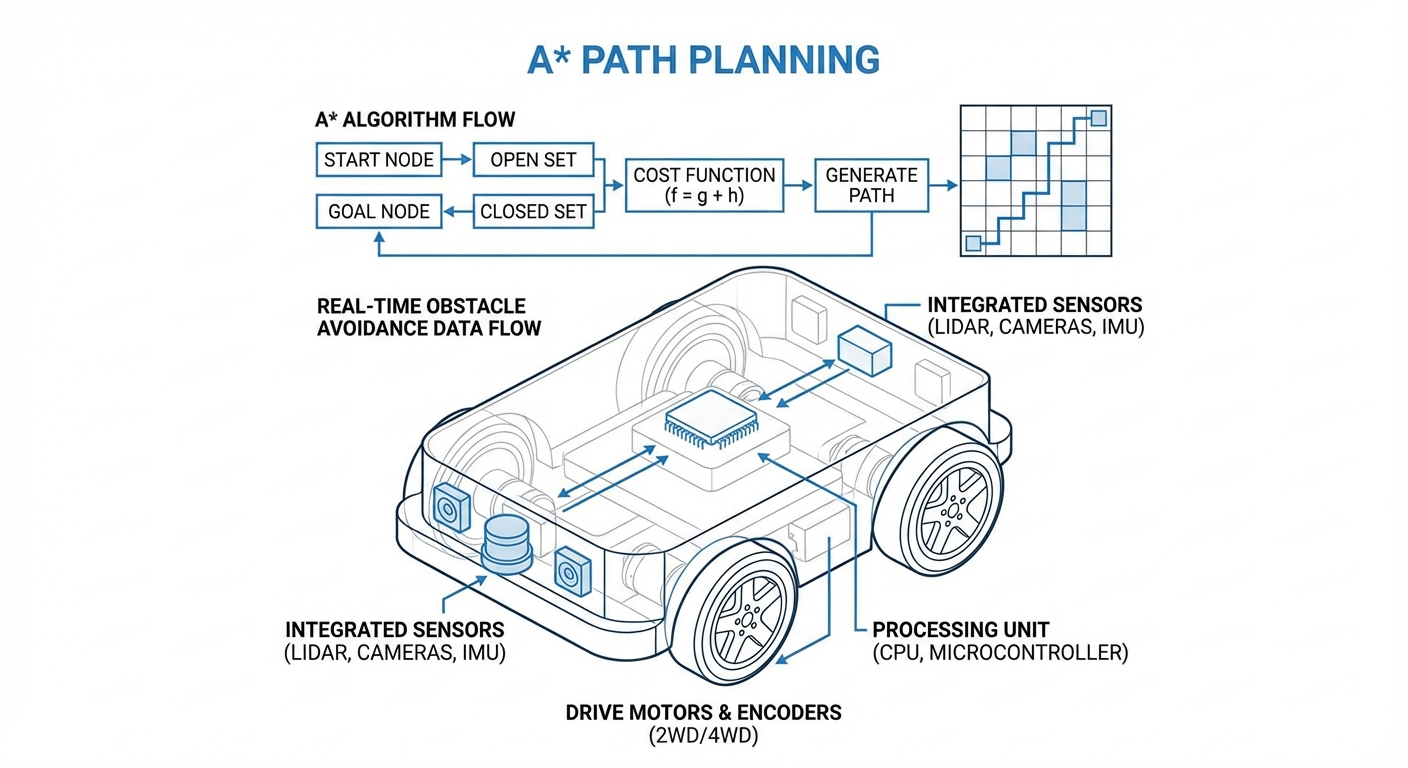
Real-World Applications
Warehouse Logistics
Perfect for crammed automated warehouses packed with hundreds of AGVs weaving through tight aisles—no gridlock—and dynamically rerouting if a path gets blocked.
Autonomous Manufacturing
A must-have for Just-In-Time (JIT) manufacturing, where mobile robots rush parts straight to assembly lines. A* nails the most efficient route to slash downtime.
Hospital Delivery AMRs
Hospital robots carting linens and meds lean on A* to navigate twisty corridors, favoring quiet zones and steering clear of hectic emergency areas.
Search and Rescue
In risky spots, rovers run A* on LIDAR maps to scout safe ways through rubble or murky terrain humans can't even see.
Frequently Asked Questions
What is the difference between A* and Dijkstra's algorithm?
Sure, both Dijkstra's and A* find the shortest path, but Dijkstra checks every direction equally (uniform search), making it slower. A* uses a heuristic to 'guess' the promising way, cranking up speed and efficiency for robotics.
How does A* handle dynamic obstacles like walking humans?
Standard A* plans static environments. For moving obstacles, AGVs kick off with A* for the global path, then layer on a local planner (like TEB or DWA) or D* Lite (Dynamic A*) to quickly replan short bits when sensors spot surprises.
What happens if no path exists to the destination?
A* is 'complete'—if there's no path, it'll scour every reachable node before calling it quits. For robots, that triggers a failure mode, so it stops and pings the operator or picks a new goal.
Is A* computationally expensive for large warehouses?
Yeah, it can guzzle memory on super-fine grids (like 1cm pixels across 1km). Devs counter with tweaks like Jump Point Search (JPS) or hierarchical planning, chunking the map into bigger zones for rough paths first.
What heuristic is best for grid-based robot navigation?
For holonomic robots that swivel any way, Euclidean distance shines. Stick to 4 directions (up, down, left, right)? Manhattan's your pick. For 8-way moves, Chebyshev diagonal distance is the go-to.
How does "Costmap Inflation" affect A* performance?
Costmap inflation pads a safety buffer around obstacles to keep the robot clear. It guarantees fit, but overdo it and tight corridors look blocked. Tune it to match the robot's actual size.
Can A* account for different terrain types (mud vs. concrete)?
You bet. Weight the G-cost (movement): 1 meter on concrete is '1', but mud? '5'. A* will skirt the mud automatically unless detouring is way longer than muscling through.
Is A* suitable for car-like robots (Ackermann steering)?
Plain A* assumes the robot can pivot in place or hop to any neighbor. For car-like steering, Hybrid A* steps in, baking the turning radius and continuous coords right into each search node's state.
What is the "Admissibility" of a heuristic?
A heuristic is admissible if it never overshoots the true cost to the goal. Stick to admissible, and A* guarantees the optimal (shortest) path. Overestimate, and it speeds up but might miss the absolute best.
Does A* work in 3D environments (drones)?
Absolutely. Ditch the 2D grid for 3D voxels (cubes). The core logic stays the same—just toss in the Z-axis for neighbors and distances—though memory skyrockets.
How do you handle "greedy" behavior in path planning?
Greedy Best-First chases just the heuristic (h), ignoring distance traveled (g). Blazing fast, but paths aren't optimal. A* strikes a balance, blending that greedy speed with careful accuracy via G + H.
What is Theta* (Theta-Star)?
Theta* upgrades A* for 'any-angle' paths. No grid-locked zigzags—instead, it checks line-of-sight to non-adjacent parents, smoothing out natural, robot-friendly routes.